leetcode 322. 零钱兑换

原创
maple
2023-07-06
leetcode
305
0

题目

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例
输入：coins = [1, 2, 5], amount = 11
输出：3 
解释：11 = 5 + 5 + 1

题解

解题思路：

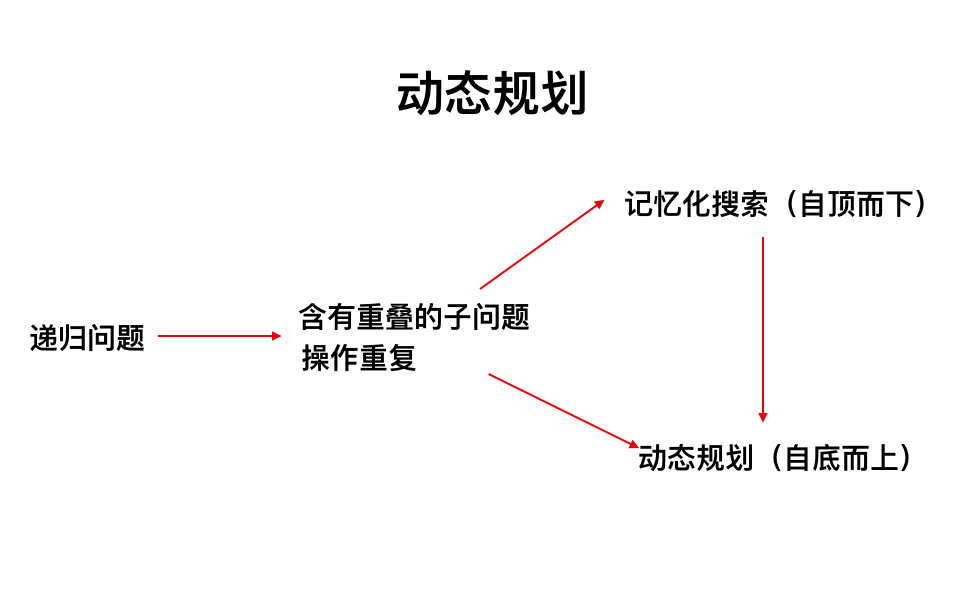
  1. 这种找路径，找方法的题一般可以使用回溯法来解决，回溯法也可以说是树形图法，解题的时候使用类似于树状图的结构，使用 自顶而下(也可以自下而上，但是自顶而下可以在后续优化成记忆化搜索提高效率) 的方法。

  2. 而在回溯法中，如果含有很多的重复的计算的时候，就可以使用记忆化的搜索，将可能出现的重复计算大状态使用一个数组来保存其值，在进行重复的计算的时候，就可以直接的调用数组中的值，较少了不必要的递归。

  3. 使用了记忆化搜索后，一般还可以进行优化，在记忆化搜索的基础上，变成 自底而上 的动态规划。

递归

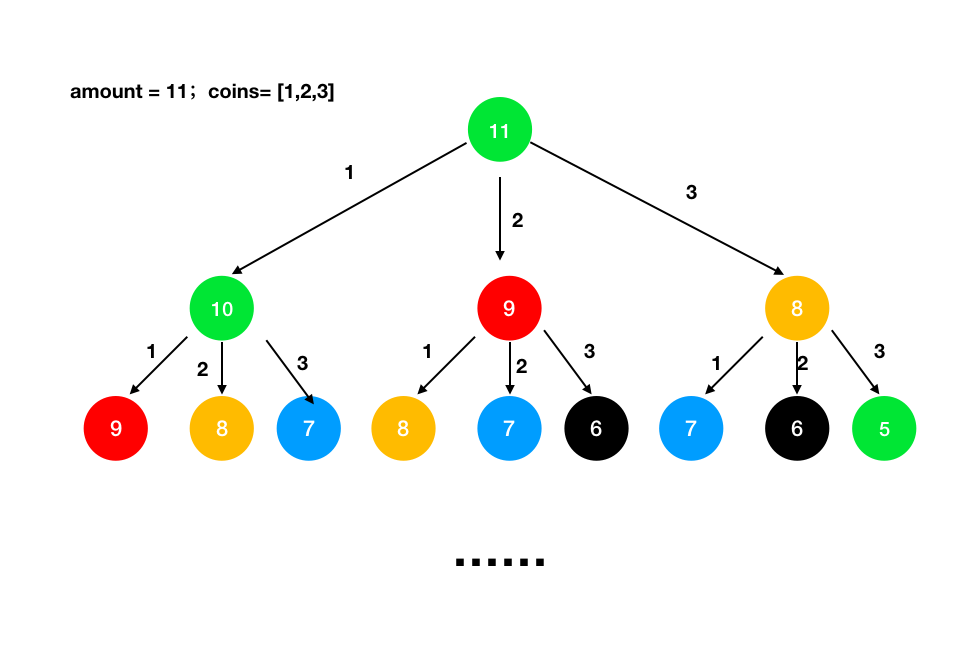
使用递归的关键是知道递归函数是用来干什么的，从宏观的角度去理解递归。 直接使用递归超出时间限制。

class Solution {
    int res = Integer.MAX_VALUE;
    public int coinChange(int[] coins, int amount) {
        if(coins.length == 0){
            return -1;
        }

        findWay(coins,amount,0);

        // 如果没有任何一种硬币组合能组成总金额，返回 -1。
        if(res == Integer.MAX_VALUE){
            return -1;
        }
        return res;
    }

    public void findWay(int[] coins,int amount,int count){
        if(amount < 0){
            return;
        }
        if(amount == 0){
            res = Math.min(res,count);
        }

        for(int i = 0;i < coins.length;i++){
            findWay(coins,amount-coins[i],count+1);
        }
    }
}

记忆化搜索

  • 可以看出在进行递归的时候，有很多重复的节点要进行操作，这样会浪费很多的时间。 使用数组 memo[] 来保存节点的值memo[n]表示钱币n可以被换取的最少的硬币数，不能换取就为 −1 , findWay 函数的目的是为了找到 amount 数量的零钱可以兑换的最少硬币数量，返回其值 int

  • 在进行递归的时候，memo[n]被复制了，就不用继续递归了，可以直接的调用。

class Solution {
    int[] memo;
    public int coinChange(int[] coins, int amount) {
        if(coins.length == 0){
            return -1;
        }
        memo = new int[amount];

        return findWay(coins,amount);
    }
    // memo[n] 表示钱币n可以被换取的最少的硬币数，不能换取就为-1
    // findWay函数的目的是为了找到 amount数量的零钱可以兑换的最少硬币数量，返回其值int
    public int findWay(int[] coins,int amount){
        if(amount < 0){
            return -1;
        }
        if(amount == 0){
            return 0;
        }
        // 记忆化的处理，memo[n]用赋予了值，就不用继续下面的循环
        // 直接的返回memo[n] 的最优值
        if(memo[amount-1] != 0){
            return memo[amount-1];
        }
        int min = Integer.MAX_VALUE;
        for(int i = 0;i < coins.length;i++){
            int res = findWay(coins,amount-coins[i]);
            if(res >= 0 && res < min){
                min = res + 1; // 加1，是为了加上得到res结果的那个步骤中，兑换的一个硬币
            }
        }
        memo[amount-1] = (min == Integer.MAX_VALUE ? -1 : min);
        return memo[amount-1];
    }
}

动态规划

  1. 上面的记忆化搜索是先从 memo[amonut−1] 开始，从上到下 动态规划从 memo[0] 开始，从下到上
  2. 转移方程 dp[n] = min{dp[n-i]+1 for i in coins if n-i >= 0 && dp[n-i] != -1}
  • c++
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount+1,-1);
        dp[0] = 0;
        for(int i = 1;i <= amount;i++){
            for(int j : coins){
                if(i - j >= 0 && dp[i-j] != -1){
                    if(dp[i] == -1)
                        dp[i] = dp[i-j] + 1;
                    else
                        dp[i] = min(dp[i-j]+1,dp[i]);
                }
            }
        }
        return dp[amount];
    }
};
  • java
class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount+1];
        Arrays.fill(dp,-1);
        dp[0] = 0;
        for(int i = 1;i <= amount;i++){
            for(int j : coins){
                if(i - j >= 0 && dp[i-j] != -1){
                    if(dp[i] == -1)
                        dp[i] = dp[i-j] + 1;
                    else
                        dp[i] = Math.min(dp[i-j]+1,dp[i]);
                }
            }
        }
        return dp[amount];
    }
}
end

评论